Théorème de Gauss (algèbre)
Théorème
Arithmétique
Lemme de Gauss (corollaire du théorème de Bézout) :
Soient \(a,b\in\Bbb Z\)
Si \(a|bc\) et \(\operatorname{pgcd}(a,b)=1\), alors \(a|c\)
(
Division - Diviseur - Divisibilité,
Pgcd)
Lemme de Gauss :
- \(a,b,c\in{\Bbb Z}\)
- \(a|bc\)
- \(\operatorname{pgcd}(a,b)=1\)
$$\Huge\implies$$
END
Démonstration :
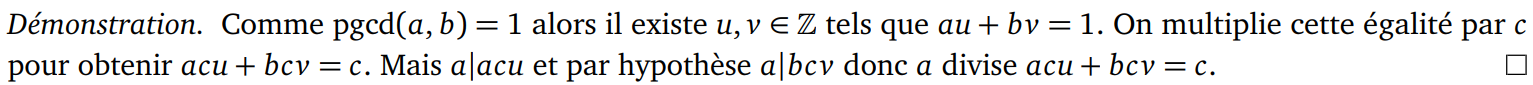
Dans un anneau
Théorème de Gauss dans un anneau :
Contenu - Polynômes primitifs
Théorème de Gauss :
Si \(P,Q\) \(\in A[X]\setminus\{0\}\), alors : $${{C(PQ)}}={{C(P)C(Q)}}$$
(
Contenu)
Théorème de Gauss (polynômes primitifs) :
"un produit de deux polynômes primitifs est primitif"
(
Polynôme primitif)